what is a in calculus Calculus pre calc math school

Calculus is a branch of mathematics that deals with rates of change and continuity. It may sound complicated, but it has real-world applications in fields like physics, engineering, and economics. It is a subject that can be challenging, but with the right approach, anyone can master it. One key concept in calculus is derivatives. A derivative is the rate at which a function changes with respect to its input variables. For example, consider the function f(x) = x^2. The derivative of this function with respect to x is 2x. This means that if x increases by a small amount, say Δx, then f(x) will increase by approximately 2xΔx. Derivatives are used in many practical applications, such as determining the speed of a moving object or the rate at which a chemical reaction is occurring. Another important concept in calculus is integrals. An integral is the accumulation of a function over an interval. For example, consider the function f(x) = 2x. The integral of this function from x=0 to x=2 is the area under the curve of the function from x=0 to x=2. This value can be calculated using a definite integral. Integrals have many practical applications, such as determining the total distance traveled by a moving object or the total amount of a chemical produced in a reaction. To better understand calculus, it is essential to study its underlying concepts, like limits and continuity. Limits are the values that a function approaches as its input variable approaches a particular value. Continuity is the property of a function where the values of the function approach its limit as the input variable approaches a particular value. These concepts are important because they allow us to define derivatives and integrals. In conclusion, calculus is a fascinating subject that has broad applications in many fields. It is challenging but rewarding to learn, as it can help us better understand the world around us. Whether you are interested in physics, engineering, or economics, calculus offers valuable insights and tools. With a solid foundation and the right approach, anyone can become proficient in calculus.

Image 1: What Is Calculus? Definition and Practical Applications

Source: thoughtco.com

Image 2: Pre-Calc\/Calculus | Jordan Larson's High School Portfolio

Source: larsonjordanportfolio.com

If you are looking for Pre-Calc/Calculus | Jordan Larson's High School Portfolio you've visit to the right web. We have 6 Pics about Pre-Calc/Calculus | Jordan Larson's High School Portfolio like Calculus - 6 Sessions - Wow Science Camp, AP Calculus – Rock on Coding, AP Computer Science, Physics, SAT Math and also What Is Calculus? Definition and Practical Applications. Here you go:

Pre-Calc/Calculus | Jordan Larson's High School Portfolio

www.larsonjordanportfolio.com

calculus pre calc math school

Calculus - 6 Sessions - Wow Science Camp

wowsciencecamp.org

calculus math maths mathematics integration sphere sessions function live

Calculus (9781464125263) | Macmillan Learning

www.macmillanlearning.com

calculus rogawski macmillan

AP Calculus – Rock On Coding, AP Computer Science, Physics, SAT Math

rockcoderacademy.com

calculus ap background math wallpaper doodle subject formula icon physics science computer useful easy vector handwriting blackboard equation mathematical theory

Calculus - Engineer4Free: The #1 Source For Free Engineering Tutorials

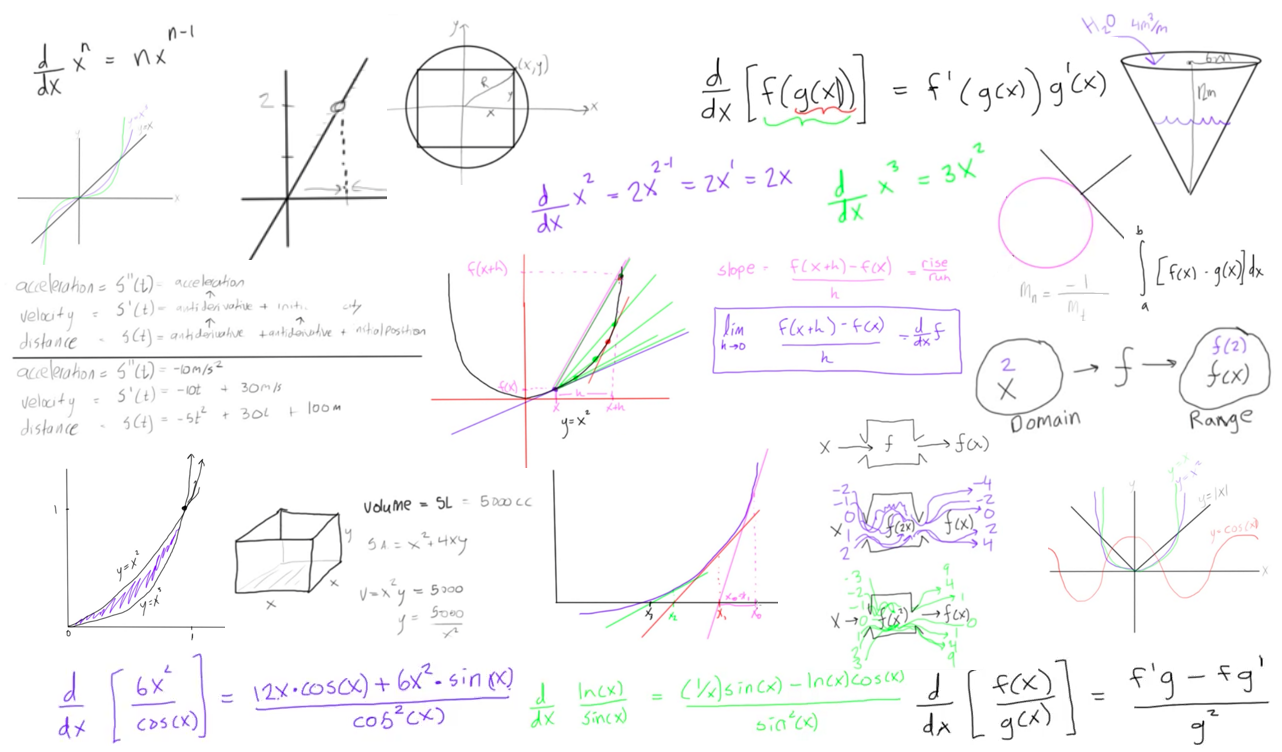www.engineer4free.com

calculus engineering tutorials course basic

What Is Calculus? Definition And Practical Applications

www.thoughtco.com

calculus blackboard definition applications practical getty source

Calculus blackboard definition applications practical getty source. Calculus ap background math wallpaper doodle subject formula icon physics science computer useful easy vector handwriting blackboard equation mathematical theory. Calculus math maths mathematics integration sphere sessions function live