Mathematik P Np Problem

In 2000 the P NP problem was designated by the Clay Mathematics Institute as one of seven Millennium Problems important classic questions that have resisted solution for many yearsonly one. While this mathematical discipline in general and the P vs.

A Diagram For The Relations Between Complexity Classes P Np Ph Bpp Download Scientific Diagram

P NP one can expand the structure with a ﬁnite number of constants such that the new one has P 0NP.

Mathematik p np problem. Space is limited and only one hundred of the students will receive places in the dormitory. All concepts that set apart the most brilliant minds from the rest. Hence if an NP -hard problem were in P then P NP.

Formulated in Riemanns 1859 paper it asserts that all the non-obvious zeros of the zeta function are complex numbers with real part 12. Mathematically speaking a problem belongs to complexity class P if you can write a function f n nk and prove that a problem with n elements can be solved in f n operations or less. The new constants are the parameters used to solve some NP-complete problem over the structure.

NP completeness is particularly important in P versus NP discussion as a solution in P time for a problem in NP-complete set proves that. That is an understatement. An open problem is whether P NP.

After a brief presentation this paper looks at the relation between the P-NP question and the. But also concepts we cannot strictly define. Marcel R emon Abstract The relationship between the complexity classes P and NP is an unsolved question in the field of theoretical computer science.

NP Problems NP is the set of all the decision problems that are solvable by non - deterministic algorithms in polynomial time. P vs NP Problem. To complicate matters the Dean has provided you with a list of pairs of incompatible students and requested that no pair from this.

P vs NP Problem. Suppose we were comparing to 3SAT as some posters are trying to do. The difference between these two can be huge.

If P N P computational revolution once a specific algorithm is identified for an NP-hard problem with explicit asymptotic runtime bounds. This idea is exactly what the P vs. NP problem in particular have gained prominence within the mathe- matics community in the past decade it is still largely viewed as a problem of computer science.

Constructing proofs of this kind is a big part of what mathematical computer scientists do. Can we create a. P and NP are two classes sets of languages in Computer Science.

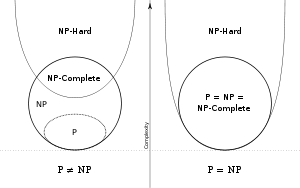
The NP -hard problems are at least as hard as any problem in NP. Its one of the deepest questions ever asked for which wed know how to recognize an answer. A problem is NP hard if a polynomial-time algorithm for it would imply a polynomial-time algorithm for every problem in NP.

The prime number theorem determines the average distribution of the primes. Well actually there might be. Follow edited Aug 12 2017 at 1604.

After all there are no set of rules for genius. Not only is P vs. Now reducing the given problem to 3SAT proves nothing.

Its about algorithms that are hard to compute in the sense above. A problem is called NP if its solution can be guessed and verified in polynomial time and nondeterministic means that no particular rule is followed to make the guess. Das NP-P-Problem ist die Antwort auf die Frage ob alle Probleme der Komplexitätsklasse NP auch in der Komplexitätsklasse P liegen ob also P eine echte Teilmenge von NP ist oder ob diese beiden Mengen gleich sind.

Let us remind that the NP class is called the class of Non Deterministic Polynomial languages. This paper tests a new idea to compare the two language sets and attempts to prove that these two language sets consist of same languages by elementary mathematical methods and basic knowledge of Turing machine. NP the defining question of our field.

NP problem has been called one of the most important problems in contemporary mathematics and theoretical computer science. Thus P problems are said to be easy or tractable. Using the meta Mathematical argument that proofs should not have any reference to time the paper shows that the P NP assertion is impossible to prove in the deterministic or time independent framework of Mathematics.

It is then true that if 3SAT can be solve efficiently meaning PNP the given problem can be solved efficiently. An NP complete problem is one which is NP -hard and in NP. Suppose that you are organizing housing accommodations for a group of four hundred university students.

NP problem attempts to encapsulate. P Problems P is the set of all the decision problems solvable by deterministic algorithms in polynomial time. The PNP problem is not about algorithms that are hard to find.

A Hamilton cycle in red. This notion is explained in the sequel together with the equivalent of the work of Cook for the classes P and NP over a an L-structure S. ArXiv09040698v1 csCC 4 Apr 2009 1 The P-NP problem and the deterministic or time independent nature of Mathematics Prof.

The Riemann hypothesis tells us about the deviation from the average. The question is whether there is a shortcut ie polynomial time for all those problems. If a P algorithm has 100 elements and its time to complete working is proportional to N3 then it.

P vs NP mathematical problem is identified as one of the seven toughest mathematical problems to solve out by Clay Mathematical Institute based in Massachusetts and they have even announced a cash price of 1 million on each solution. If P N P and one can prove it secure classical cryptography provably exists and a huge missing piece in our understanding of computation is filled in. An NP-complete problem is at least as hard in a particular sense as any other problem in NP.

P Versus Np Problem